Understanding Assembly Indices
Calculating the Assembly Index of a molecule is an NP-Hard problem. We've developed a hierarchy of algorthmic approaches to this calculation. Use the descriptions below to understand the outputs from Molecular-Assembly.com.
Molecular Assembly Indices
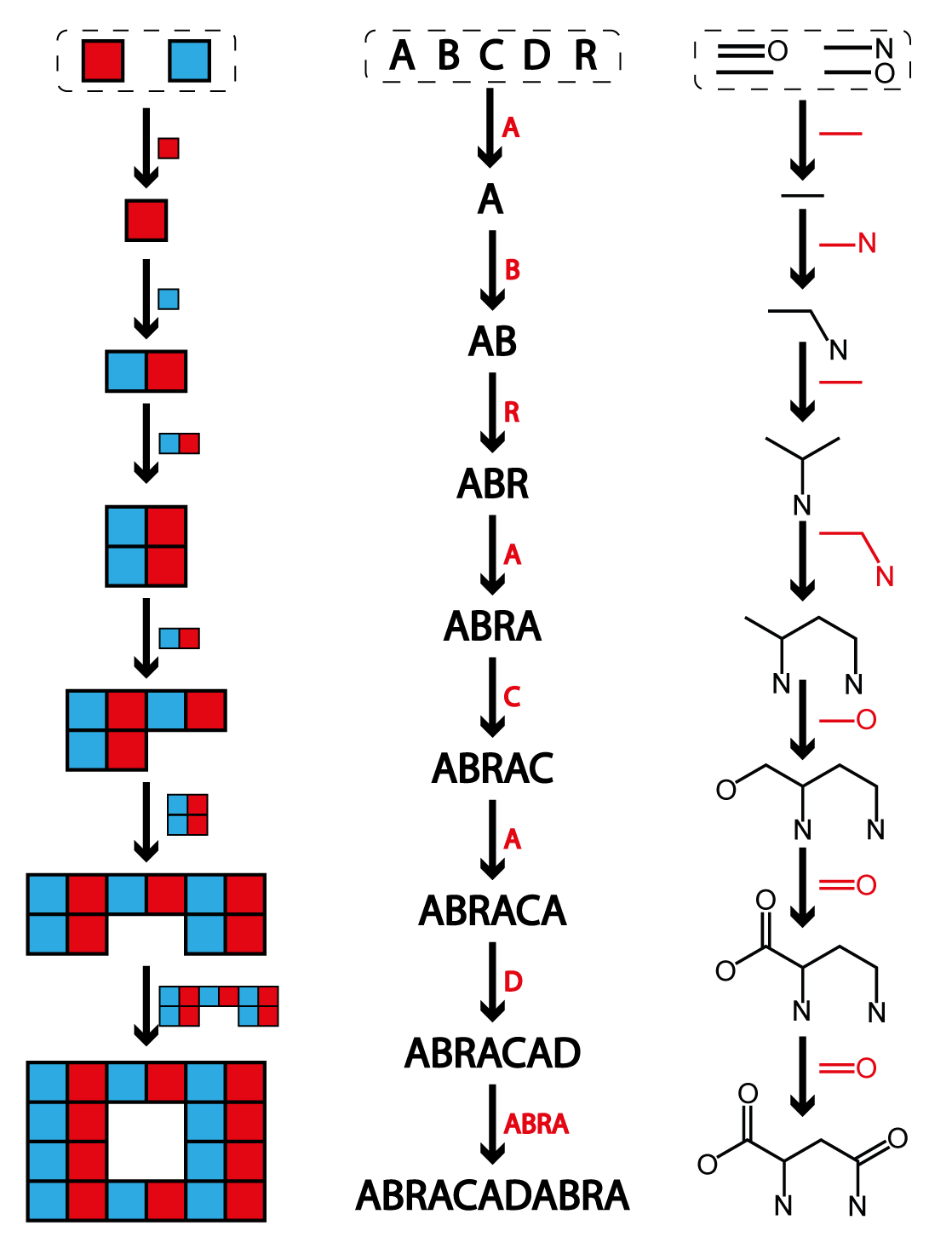
Molecular Assembly indices are a fundamental quantity in Assembly Theory because they measure
the amount of information required to make a molecule. The Molecular Assembly Index (MA) of a
molecule is defined as the fewest number of steps required to make the molecular graph
by recursively using previously made structures. Let's unpack that statement a bit.
First let's get a feel for this process. Instead of thinking
about molecules, let's consider the Assembly Index of a word, like "ABRACADABRA". This example
is
worked out in the image on this page. The word contains eleven letters in total, but is built of
four unique letters ("A", "B", "C", "R"). We'll refer to the unique letters in the word as the
"basic building blocks." To start the assembly process we can take a basic building block, in
this case let's start with "A" which we can join with another
building block, "B", to make "AB", that's one step. We can repeat this process a couple times
to make "ABRA", and then a few steps later we will have made "ABRACAD". So far the number of
steps we have taken is six, which is the length of the word we've made so far. To finish the word
we need to add four more letters, but we've previously made the remaining piece we need ("ABRA"),
so we can add all of those in one step, resulting in an Assembly Index of 7. That last step,
where we reused "ABRA", is what we mean when we say "recursively using previously made
structures." We could have taken a longer path to make the final word, for example by reusing
"AB" but adding "R" and "A" at the end in seperate steps. That would have taken a total of 9
steps. When we say the Assembly index is the "fewest number of steps" what we mean is that
there is no way to make the final target using fewer steps - although there might be pathways
that require the same number of steps (for example you can build ABRACADABRA from right to left
instead of left to right in the same number of steps).
We when talk about the Molecular Assembly Index (MA) of a molecule we are talking about the
steps required to make its graph structure, not the molecule itself. That means that we are not
concerned with whether or not the operations we perform in this process could be physically
done in a lab or a natural setting. Therefore some of the joining operations could seem
counterintuitive to chemists or folks who make real molecules for a living. The number of steps
required to make the graph will never be less than the number of individual mechanistic steps
required to make the actual molecule. This is why we emphasize that we are calculating the fewest
number of steps to make the molecular graph, not the molecule. When we compute the MA of a
molecule we ignore the Hydrogen atoms. This is done primarily for computational simplicity
because it significantly reduces the number of atoms in a molecule and has an insignificant
effect on the structure of the compounds. Finally when we consider the basic building blocks of
a molecule, we use the unique bonds in the molecule, not the atoms, as the components. That
means that joining operations are defined by super imposing two (or more) atoms in different
bonds.
Computing the MA of a compound is an NP-Hard problem,
meaning that the computational time required to find the answer increases significantly with the size of
the molecule. This is one reason we have decided to have Molecular-Assembly.com look-up precomputed MA values for
molecules rather than compute them de-novo. In order to understand the data that this website
provides it is important to understand the different algorithms we have developed to calculate
MA. We detail the those algorithms below.
Exact MA
Although we aim to find the shortest pathway required to construct a graph from two-bond fragments, the
graph assembly algorithm does not directly calculate the assembly index by searching through the space of
possible pathways. Rather, it attempts to find duplicatable subgraphs in the molecule-graph and iteratively
removes subgraphs.

At each step of the process, we find a duplicatable subgraph within the molecule graph. We then remove this
duplicatable subgraph from the structure by deleting all edges (but not nodes) from the original graph and
disconnect the replicated structure associated with the duplicatable subgraph from the remnant structure.
We continue this process until no possible duplicatable subgraphs remain.
The maximum possible assembly index for a graph is N–1, where N is the number of edges in the graph. Such
a graph has no duplicatable subgraphs with at least two bonds. In order to calculate the assembly index using
this duplicate-finding method, for each duplicatable subgraph deleted, we subtract from the N–1 upper bound
the value k–1 where k is the number of edges in the subgraph. This is because each duplicate of size k represents
a saving of k–1 bonds over a one-bond fragment during the forward assembly process. The sum of all k–1 values for
all possible duplicates S can be subtracted from N–1 to obtain the assembly index for a particular molecule.

The graph assembly algorithm seeks to find the shortest assembly pathway and does so by finding the pathway with
the largest value of S. Broadly, it does so by first finding all possible duplicatable subgraphs in the initial
graph. All the duplicate graphs are grown and classified as unique via the VF2 graph isomorphism. Those duplicated
subgraphs are sorted and fragmented according to duplicates in reverse order of size using a modified disjoint-set
data structure. Finally, the fragments are recursively hashed into a Hash assembly state and pruned with a tight
branch and bound strategy. This process is done until convergence, and at each step, the best construction pathway
is stored for retrieval. Note that if the process is stopped early, then the assembly index is labeled as approximate,
even if it is the actual value.
For more details on the algorithm and the pathway generation see the paper:
Rapid Exploration of the Assembly Chemical Space of Molecular Graphs
and the associated supplement.
